Despedida

Queridos alumnos:

Después de tanto trabajo, hemos llegado al final de ésta unidad, espero que les haya gustado trabajar de esta manera.

                                                            

Por acompañarme en este blog

Expresiones Algebraicas Racionales Fraccionarias

Una expresión algebraica fraccionaria es una expresión de la forma: 

siendo el grado de  mayor o igual que uno (con esto quedan excluidos el polinomio nulo y todos los polinomios de grado cero).

Se puede operar con las expresiones algebraicas fraccionarias y se lo hace de igual modo a como se suman, restan, multiplican y dividen las fracciones numéricas.

Simplificación:

Una de las aplicaciones más importantes del principio fundamental de las expresiones algebraicas es la de reducir una fracción a su mínima expresión.

Operaciones con polinomios

Adición de polinomios

 La  suma  de  dos  o  más  polinomios  es  otro  polinomio  cuyos  términos  se  obtienen sumando los términos de igual grado.

Diferencia de polinomios

Para restar el polinomio Q(x) del polinomio P(x)  se debe sumar al polinomio P(x)  el opuesto de Q(x):

Producto de polinomios

Para multiplicar dos polinomios se multiplica cada monomio de uno de ellos por cada uno de los términos del otro y luego se suman los coeficientes de los términos de igual grado (para operar se deben tener en cuenta las propiedades distributiva del producto respecto de la suma de números reales y del producto de potencias de igual base).

¡Algunos productos notables!

Hacer click aquí para ver las actividades: ACTIVIDAD N°2

División de polinomios

Para efectuar la división entre dos polinomios, el polinomio dividendo debe ser de grado mayor o igual que el grado del polinomio divisor y deben estar ordenados en forma decreciente. Además el polinomio dividendo debe estar completo.

Si no comprendieron bien la división de polinomios, aquí les dejo este video para que lo vean. Espero que les sirva de ayuda para resolver todas sus dudas, cualquier consulta lo vemos en clases.

Hacer click aquí para ver las actividades: ACTIVIDAD N°3
Alumnos ahí les dejo la actividad,tienen que traer para la próxima clase y lo vamos a resolver entre todos. 
Pueden visitar las siguientes páginas se trata sobre suma y multiplicación de polinomios

Está es la direccion: http://www.vitutor.com/ab/p/a_5.html

http://www.vitutor.com/ab/p/a_6.html

Factorización de Polinomios

Si  dos  expresiones  algebraicas    A  y  B  se multiplican  y  su  producto  es  C,  es  decir: A.B=C, cada una de las expresiones algebraicas  A y B es un factor de C. 

Factorear o factorizar una expresión algebraica es expresarla como producto de sus factores primos.  

¡Alumnos! a continuación les dejo una presentación sobre los diferentes casos de factoreo que les servirá de apoyo para resolver las actividades que tienen que traer resueltas para la próxima clase.

Trabajo de practico nº2 from BarbozaValeriaPaola

A tener en cuenta!

En algunas expresiones se podrá aplicar, en forma sucesiva, más de un caso de factoreo. 

Para resolver estos ejercicios se sugiere factorear en el siguiente orden:

1.  Buscar factor común, ya sea único o por grupos. 

2.  Si el polinomio tiene dos términos buscar diferencias de cuadrados o suma o diferencia de potencias de igual grado. 

3.  Si tiene tres términos puede ser el cuadrado de un binomio. 

4.  Si tiene cuatro términos puede ser el cubo de un binomio.  

Alumnos aquí les dejo la siguiente actividad, que controlaremos la próxima clase. Miren el  power que le servirá de ayuda para resolver las actividades.

Hacer click aquí para ver las actividades: ACTIVIDAD N°4

Comenzamos a trabajar!!!

Polinomio en una variable:

Se  llama  polinomio  de  grado  n  en  la  variable  (o  indeterminada), sobre  el conjunto de los números reales, a toda expresión de la forma:

Polinomios

Se llama polinomio a toda expresión algebraica racional entera.

Ejemplo:

De  acuerdo  con  la  cantidad  de  términos  que  poseen  los  polinomios  algunos  reciben nombres especiales:

• monomio si tiene 1 términos

• binomio si tiene 2 términos

• trinomio si tiene 3 términos

• cuatrinomio si tiene 4 términos 

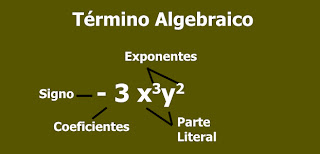
Observar  que cada término de un polinomio es un monomio y está  formado por una parte numérica llamada coeficiente y una parte literal.

                                                                                                                                                                                         

Importante:

•  El  grado  de  un  monomio  es  la  suma  de  los  exponentes  de  las  variables (o indeterminada) que contenga.

• El  grado  de  un  polinomio  es  el  grado  del  monomio  de  mayor  grado  que participa en él.

• Un  polinomio  es  homogéneo  cuando  todos  sus  términos  son  del  mismo grado.

Nota:  Trabajaremos con polinomios en una variable.

Chicos acá les dejo la primer actividad, para poner en practica lo que estuvimos viendo. Cualquier duda que tengan lo vemos en la clase que viene.

Hacer CLICK aquí para ver las actividades: ACTIVIDAD N° 1

Expresiones Algebraicas

Se  llama expresión algebraica  a  toda  combinación de números y  letras vinculados por las operaciones de suma, resta, multiplicación, división, potenciación y radicación.

Ejemplo: